In the practise the relation that we are going to approximate respresents an “ideal situation“, which is unreachable due to our limited expressing power (i.e. constrained vocabulary given by interpretability, incorporated vagueness, display resolution, computational precision etc.). Therefore, we admit some imprecision or an error of expressing the given situation to compensate it by readibility and simplicity of the final output. This output can take one of the following two forms (formalization introduced in [1]):
Notation | Formalization
| Simplified interpretation
|
Disjunctive NF | DNF(x) =∪ iεIR(ci,x)&F(ci) | At most F1/x is close to c1 OR …OR At most Fn/x is close to cn |
Conjunctive NF | CNF(x) = ∩iεIR(x,ci)→F(ci) | At least F1/x is not close to c1 AND … AND At least Fn/x is not close to cn |
I = 1, … , n,
F – relation representing ideal situation and Fi = F(ci),
c1,…, cn – nodes,
R - fuzzy relation used to describe neighobourhoods of the nodes,
& - interpretation of the logical connective for strong conjunction,
∪ - interpretation of the logical connective for lattice disjunction,
∩ - interpretation of the logical connective for lattice conjunction,
→ - interpretation of the logical connective for implication.
As can be observed from the simplified linguistic interpretation (for the details see [2]) of the both normal forms, they can be used only in the specific applications, where the variable x denotes some quantity with an ordered scale of values (weight, preasure, grey scale, variance etc.). Moreover, we still have two free parameters: the fuzzy relation R and a distribution of the nodes over the domain of F. These parameters can be tuned to receive the best possible results with respect to a chosen criterion, e.g. minimal difference of NF from the ideal relation F, maximal degree of a fuzzy equivalence (or proximity measure) between NF and F, or minimal distance measure. This naturally leads to an optimization search process. In this field Genetic Algorithms (GA) are the best known and the most widely used global search techniques capable of finding near optimal solutions in complex search spaces.
![]()
There may be various optimizing tools used in this problematic such as neural networks, evolutionary algorithms etc. GA were chosen due to their sufficitently good behaviour in a huge rearch space.
In this special application, we use a performance measure of GA based on the fuzzy equivalence ↔ defined by x↔y = (x→y)&(y→x) and our optimizing problem is formulated as follows
a) Find c1,…, cn such that min xεD (F(x) ↔ DNF(x)) is maximal.b) Find c1,…, cn such that min x ε D (F(x) ↔ CNF(x)) is maximal.
Due to the different character of DNF and CNF, we cannot expect that the solutions will be identical. It turned out that in the problem a) the nodes have tendency to locate in the global maximas, while in the case of b) the nodes tend to be global minimas, or at least near by. It is neccessary to keep on mind that this explanation is simplified and practically the numer of the nodes needs to be incorporated.
Example:
Let us consider n = 6, F(x) = (1+exp(x2)cos(36x))/2 on [0, 1], & be the Lukasiewicz t-norm, and R(x,y) = (x→y)k(x,y)&(y→x)l(x,y).
Applying the genetic algorithm, we have obtained
C = {ci| iεI} = {0.1795, 0.5039, 0.689, 0.3307, 0.83, 0.0264} and C' = {c'i| iεI} = {0.4374, 0.2605, 0.957, 0.7866, 0.0873, 0.6054}for which we had
i | 1 | 2 | 3 | 4 | 5 | 6 |
ki=k(ci,x) li=l(ci,x) | 12 14 | 13 7 | 10 7 | 15 8 | 10 2 | 3 18 |
k'i=k(x,ci) l'i=l(x,ci) | 11 11 | 12 13 | 4 6 | 7 8 | 13 13 | 8 11 |
The final approximations are
DNF(x) =∪ iεI (ci→x)ki&(x→ci)li&F(ci),
CNF(x) = ∩ iεI (c‘i→x)l′i&(x→c′i)k′i→F(c′i),
depicted below
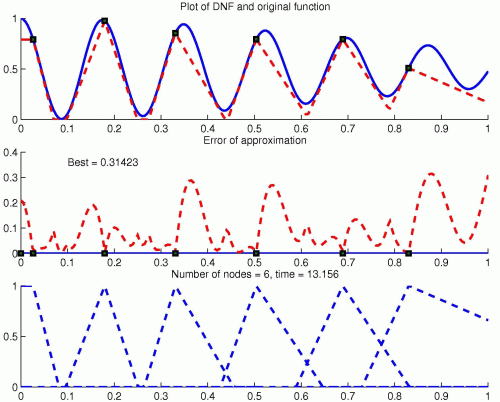
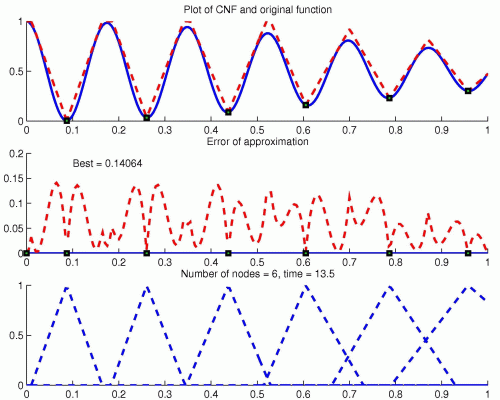
i | 1 | 2 | 3 | 4 | 5 | 6 |
ki=k(ci,x) li=l(ci,x) | 7 6 | 5 11 | 15 9 | 0 17 | 8 12 | 1 0 |
k'i=k(x,ci) l'i=l(x,ci) | 13 14 | 5 6 | 12 13 | 8 7 | 8 1 | 8 11 |
Click to view the demonstration for DNF (EXE file) and CNF (EXE file).
Related links:
Research reports
67. Martina Daňková, Martin Štěpnička: Genetic Algorithms in Fuzzy Approximation, 2004. Download Report 67.
94. Martina Daňková: On Approximate Reasoning with Graded Rules, 2006. Download Report 94.
Technical reports
5. Martina Daňková: Data driven learning algorithm for normal form based fuzzy rules, 2005
References
[1] I. Perfilieva, Functions Represented by BL-Algebra Formulas: Characterization and Approximate Representation. In Soft Computing. 2005, 9, pp.910-918.
[2] M. Daňková, On approximate reasoning with graded rules. In Fuzzy Sets and Systems. 2007, 158, pp. 652-673.


