Introduction
In classical mathematics, various kinds of transforms (Fourier, Laplace, intergral, wawelet) are used as powerful methods for construction of approximation models and their further utilization. The main idea of these transforms consists in transforming the original model into a special space where the computation is simpler. The transform back to the original space produces an approximate model or an approximate solution. There is a bridge put between these well known classical methods and methods for construction of fuzzy approximation models in this research. We have developed the general method called fuzzy transform (or shortly F-Transform) that encompasses both classical transforms as well as approximation methods based on elaboration of fuzzy IF-THEN rules studiet in fuzzy modeling.
This transform we used, i.a., in image processing, especially in image compression and image fusion.
Image compression
The basic idea is to use the forward fuzzy transform as the main process in image compression. Generally, an image is represented by a set of pixels. Algorithm takes this set of pixels as an input into the forward discrete fuzzy transform; the result is the set of components representing the source image. Those components can be processed by any further alghorithm and finally saved to the file representing source image. Backwards, to reload the image from the file, the components are loaded from the source file, and passed as an input into the inverse dicrete fuzzy transform. A result produced out of the transform is a set of pixels representing the source image.
The basic of this application is the discrete fuzzy transform. It has been published e.g. in [1]. The fuzzy transform delas with a continuous function but it has also its discrete version; in image processing pixels are viewed as discrete function values from the interval <0, 255>. Therefore the discrete fuzzy transform has to be used. Its components are defined as follows:
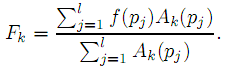
where pj are nodes from interval [a; b] and Ak (for k > l) are basic functions which form a fuzzy partition of [a, b]. The inverse fuzzy transform has been defined as follows:
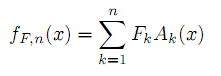
The weak point of the discrete fuzzy transform is sharp edge. In image processing this case happens where big color/contrast changes occur. The main principle of the compression is shown on the image below:
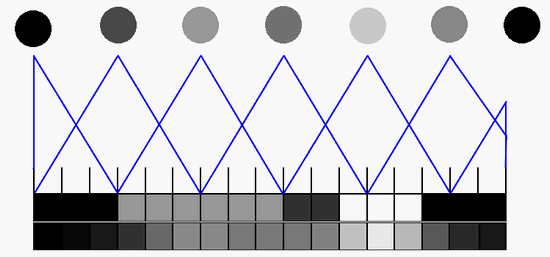
As mentioned before, set of pixels (discrete values) are taken as a source for the fuzzy transform. Components are calculated from these pixels.
"How many pixeles is covered by one component" is the main unknown variable in this process. The higher the value, the lower final count of components (that means better compression), but also decreases the quality of the reconstructed image; and vice-versa.
As shown on the image, both pixels closest to each other at an edge affect each other. The bigger the difference between source pixels, the bigger the defection on the reconstructed pixels. This effect causes the reconstructed image to be fuzzy.

Therefore there are some algorithm improvements made to deal with this behavior, mainly:
-
Use two (or alternativery more) components at the edges, where change between pixels is too significant. The rest of the image is described by only one component layer;
-
Try to find the similar parts of the image and low number of components is applied at those whole parts;
-
At color images the each part of image (e.g. red/green/blue) is compressed separately. There is a place to express those components which are more significant for human colour perception and supress components which are not. Therefore also YCrCb model has later used to do this.
As presented here, windows desktop application, FIC (Fuzzy Image Compression) has been developed and is described in Tools section.
Related links:
Research reports
[1] Research report 58. Irina Perfilieva: Fuzzy Transforms, 2004. Download Report 58.
[2] Research report 119. Irina Perfilieva, Viktor Pavliska, Marek Vajgl, Bernard De Baets: Advanced Image Compression on the Basis of Fuzzy Transforms, 2008. Download Report 119.
Chapters in monographs
[3] I. Perfilieva, Fuzzy Transforms and Their Applications to Image Compression, in: Springer, Heidelberg, 2006, pp. 19-31.


