1. Introduction to the problem
Fuzzy modeling tools may be applied to solve several kinds of tasks which have a common denominator vagueness. The following task belong among the typical ones solved by advanced fuzzy modeling tools:
- Fuzzy control
- Decision making
- Object classification and pattern recognition
- Approximation of functions
Practical problems are usually too complex and difficult to be modeled only by one technique, therefore a combination of several approaches is used to design system for solving the task. It turns out to be practically necessary to use such tools, which enable to design hierarchical and heterogeneous systems.
2. Focus of our research
Our research aims at developing such a tool, which satisfies the above requirements. Theoretical background of particular elements is, of course, based mainly on fuzzy set theory, but for design of whole compound system are used techniques based on graphical programming which has roots mainly in petri nets [5,6].
For this purpose, we extended the concept of the classical petri nets to fuzzy petri net (FPN) [4,7] which may be used for the design and a visualization of the hierarchical system composed by interconnected sets of fuzzy IF–THEN rules [3]. In FPN, a token serves as a carrier of a fuzzy set, edges are evaluated by linguistic expressions [1] which occur in a given set of fuzzy IF THEN rules and finally, transitions represent basically fuzzy relations according to the respective fuzzy IF THEN rules. Construction of the fuzzy reation is dependent on a chosen inference method. For more details, see the description of the software package LFLC 2000 and [1,2,3].
Let us consider the following example of a correspondence between IF-THEN rules and petri nets:
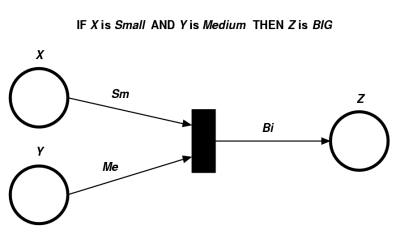
3. Description of the main results
For the present, the main result in this area is the tool, which involves an algorithm for a decomposition of an acyclic fuzzy petri net into a set of linguistic descriptions, which form the so called Linguistic Fuzzy Logic Net (LFLN). An input of this algorithm is a fuzzy petri net and its output is a set of linguistic descriptions corresponding to each output place of fuzzy petri net.
This algorithm is implemented in a tool fpn2lfln, which takes a file generated by The Petri Net Kernel (PNK 2.0) in PNML (XML) format as an input. Developed tool fpn2lfln internally converts given fuzzy Petri Net into Linguistic Fuzzy Logic Net (LFLN). Finally, all output variables of LFLN are evaluated and a user is provided with the results.
4. Further development
The designing and the visualization of fuzzy IF–THEN rules by means of fuzzy Petri nets is only a small step to the final goal - to make the user-friendly design of hierarchical structures possible. This task may consist of various kinds of units, each of them possibly performing a different inference mechanism.
A possibility to visually design own system or visually modify a predefined typical system composed from basic elements provided with the whole software package is the main advantage for users. Due to principles of graphical programming, users of such a system are provided by incomparable possibilities and by incomparable flexibility in comparison with classical systems.
References:
[1] NOVÁK, V.: A Comprehensive Theory of Trichotomous Evaluative Linguistic Expressions. In S. Gottwald, P. Hájek, U. Höhle, and E. P. Klement, editors, Proc. of 26th Linz Seminar on Fuzzy Set Theory. (to appear). Research Report No. 71.
[2] NOVÁK, V., PERFILIEVA, I.: On the semantics of perception–based fuzzy logic deduction. International Journal of Intelligent Systems, 19:1007–1031, 2004. Research Report No. 51.
[3] NOVÁK, V., LEHMKE, S.: Logical structure of fuzzy IF–THEN rules. Fuzzy Sets and Systems, 157:2003–2029, 2006. Research Report No. 69.
[4] KNYBEL, J., PAVLISKA, V.: Representation of Fuzzy IF-THEN rules by Petri Nets. ASIS 2005, MARQ, s. 121-125. ISBN 80-86840-16-6, 2005. Research Report No. 84.
[5] ČEŠKA, M.: Petriho sítě, Academic publisher CERM, Brno, 1994 (in Czech).
[6] PETERSON, J.L.: Petri Net Theory and the Modeling of Systems, Prentice-Hall, N.J., 1981, ISBN 0-13-661983-5.


