Developing new evolutionary algorithms for global optimization in fuzzy models

1 Introduction to the problem The global optimization problem with box constraints follows the form:

minimize f(x) subject to x ε D

where x is a continuous variable with the domain D from R^d, and f(x) : D→ R is a continuous function. The domain D is defined by specifying lower (a_j) and upper (b_j) limits of each component j,

D=∏_i=1 [a_j,b_j], a_j < b_j, j=1,2,...,d .

The global minimum point

is the solution of the problem.

Both the stochastic search and the evolutionary algorithms adapt the current search strategy that was gathered from the search up to the present time. The adaptation in the evolutionary algorithms is mainly focused on a population of individuals (points in D). Attempts that include self-adaptive mechanisms into the core of algorithms were presented in recent years. These mechanisms are based on the competition and cooperation of heuristic evolutionary operators. In spite of the No Free Lunch theorems indicating the same performance of all the search algorithms over the set of possible optimization problems empirical comparisons imply that the self-adaptive algorithms outperform others in many optimization problems.

2. Focus of our research Our research is focused on the following topics:

• development of the self-adaptive variants of controlled random search and its applications to the estimation of parameters in nonlinear regression models,
• research on the self-adaptation of control parameters in the algorithm of differential evolution,
• development of program libraries with self-adaptive algorithms for the global optimization that are applicable to real-word problems,
• methods for numerical testing of stochastic algorithms and statistical evaluation of results,
• application of evolutionary algorithms to optimization of fuzzy models.

3. Description of the main results

• randomized reflection in simplex (1995),
• evolutionary search (1996),
• application to computational statistics and shape optimization (2000 and later),
• competition of local heuristics in CRS (2001),
• self-adaptation in CRS and evolutionary search (2002 and later),
• self-adaptive CRS for nonlinear regression (2006),
• adaptation of control parameters in differential evolution (2006),
• Program Library in Matlab (2007).

4. Demonstration

Several adaptive evolutionary algorithms are implemented in Matlab as Program Library and they can be downloaded at http://albert.osu.cz/oukip/optimization/.

Self-Adaptive Differential Ecolution with Competitive Control Parameter Setting

The differential evolution (DE) has become one of the most popular algorithms for the continuous global optimization problems in last decade. However, it is known that the efficiency of the search for the global minimum is very sensitive to the setting of its control parameters. That is why the self-adaptive DE was proposed and included into this library.

How to use Matlab Program Library?

1. Problem Specification and Algorithm Description – see matlib_decomp.pdf
2. Download the zipped codes from de_competitive.zip
3. Unzip the packed files into the directory at your harddisk.
4. The objective function must be written as m-file in Matlab, placed in the same directory
5. The name of this m-file and the name of function are identical.
6. Run the optimization process

Illustrative Example

For illustration of finding global minima will be used Schwefel's function, which is multimodal and the global minimum is distant from the next best local minima:

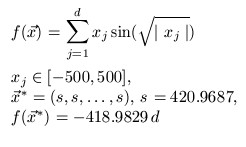
Code of Schwefel’s function in Matlab:

function y=schwefel(x)
% Schwefel's function, <-500,500>,
% glob. min f(x_star)=-418.9829*d, x_star=[s,s,...,s], s=420.97
d=length(x);
sz=size(x);
if sz(1)==1 x=x'; end
y=-sum(x.*sin(sqrt(abs(x))));

Calling sequence in Matlab – algorithm DEBR18:

Specification of the search space D:
>> b=500*ones(1,2); a=-b;

Call of optimization algorithm (only with obligatory input parameters):
>> [x_star,fn_star,ne]= debr18('schwefel',a,b)

Displayed results of optimization process:
x_star = 420.9687 420.9688
fn_star = -837.9658
ne = 1740

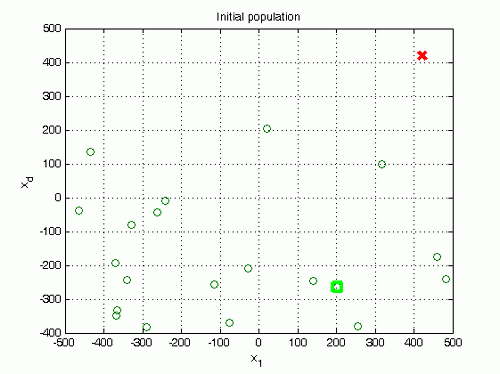
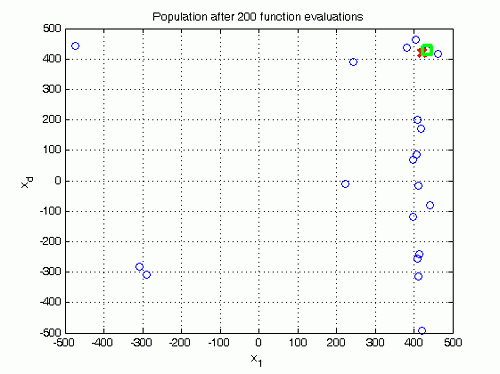
Illustrative plots of optimization process – development of population:

Legend to the figures:

red cross – the global optimum point (it does not belong to the population, its approximation is searched for)
green square – the point with minimum function value in the current population

References

[1] Haslinger, J., Jedelský, D., Kozubek, T., Tvrdík, J. Genetic and Random Search Methods in Optimal Shape Design Problems, J. Global Optimization, 2000, 16, 109-131. [2] Krivý, I., Tvrdík, J. The Controlled Random Search Algorithm in Optimizing Regression Models. Comput. Statist. and Data Anal., 1995, 20(2), 229-234. [3] Krivý I., Tvrdík J. Stochastic Algorithms in Estimating Regression Models, 12th symposium of COMPSTAT, August 1996, Barcelona, In: COMPSTAT 1996, Proceedings in Computational Statistics (ed. A. Prat), Physica Verlag, Heidelberg, 1996, 325-330. [4] Krivý, I., Tvrdík, J., Krpec, R. Stochastic algorithms in nonlinear regression, Comput. Statist. Data Anal., 2000, 33, 278-290. [5] Krivý, I., Tvrdík, J. Stochastic optimization in smoothing time series of labour market descriptors. In: Bulletin of ISI, Tome LIX, Book 1 - Contributed Papers, ISI Press, Seoul, 2001, 253-254. [6] Misík, L. On Convergence of a Class of Evolutionary Algorithms. In: Proceedings of MENDEL 2000, 6th International Conference on Soft Computing, Technical University Press, Brno, 2000, 97-100. [7] Misík, L., Tvrdík J., Krivý, I. On Convergence of a Class of Stochastic Algorithms. In: Antoch, J. and Dohnal, G. (Eds.), Proceedings of ROBUST 2000, JCMF Press, Prague, 2001, 198-209. [8] Tvrdík J., Krivý I. A Genetic Type Algorithm for Optimization, MENDEL'96, 2nd International Conference on Genetic Algorithms, In: MENDEL'96, Technical University, Brno, 1996, 176-180. [9] Tvrdík J., Krivý I. Evolution Algorithms in Regression. In Bulletin of International Statistical Institute 51st Session Proceedings, Tome LVII (invited papers), Book 2, 1997, 37-40. [10] Tvrdík, J., Krivý, I. Simple Evolutionary Heuristics for Global Optimization, Comput. Statist. Data Anal. (in SSN), 1999, 30, 345-352. [11] Tvrdík, J., Krivý, I., Misík, L. Evolutionary algorithm with competing heuristics. In: Osmera, P. (ed) MENDEL 2001, 7th International Conference on Soft Computing. Technical University, Brno, 2001, 58 - 64. [12] Tvrdík, J., Misík, L., Krivý, I. Competing heuristics in evolutionary algorithms. In: Sincák, P. et al. (eds) Intelligent Technologies - Theory and Applications. IOS Press, Amsterdam, 2002, 159 - 165. [13] Tvrdík J., Krivý I. and Misík L. Evolutionary algorithm with competing heuristics in computational statistics. Compstat 2002, Physica-Verlag, Heidelberg, 2002, 349 - 354. [14] Tvrdík, J., Krivý, I. Comparison of algorithms for nonlinear regression estimates. In: Antoch, J. (ed) COMPSTAT 2004. Physica-Verlag, Heidelberg New York, 2004, 1917 - 1924. [15] Tvrdík J. Generalized controlled random search and competing heuristics. MENDEL 2004, 10th International Conference on Soft Computing, (Matousek R. and Osmera P. eds). University of Technology, Brno, 2004, 228 - 233. [16] Tvrdík, J. Competition and cooperation in evolutionary algorithms: A comparative study. In: Proceedings of MENDEL 2005, 11-th Int. Conference on Soft Computing (Matousek R. and Osmera P. eds), Technical University Press, Brno, 2005, 108 - 113. [17] Tvrdík, J., Krivý, I., Misík, L. Adaptive population-based algorithm for global optimization. In: Ricci, A. and Vichi, M. (eds), COMPSTAT 2006. Physica-Verlag, Heidelberg New York, 2006, 1363 - 1370. [18] Tvrdík, J. Competitive Differential Evolution. MENDEL 2006, 12th International Conference on Soft Computing (Matousek R. and Osmera P. eds). University of Technology, Brno, 2006 7 - 12. [19] Tvrdík, J. Competitive differential evolution and genetic algorithm in GA-DS Toolbox. In Technical Computing Prague 2006. Praha, Humusoft, 2006, 99 -'99. Full version available at http://dsp.vscht.cz/konference_matlab/MATLAB06/prispevky/tvrdik/tvrdik.pdf. [20] Tvrdík, J. Differential Evolution: Competitive Setting of Control Parameters, Proceedings International Multiconference on Computer Science and Information Technology, Wisla, Poland, 2006, 207 - 213. [21] Tvrdík, J., Krivý, I., Misík, L. Adaptive Population-based Search: Application to Estimation of Nonlinear Regression Parameters, Computational Statistics and Data Analysis (2007) doi 10.1016/j.csda.2006.10.014 (in print). [22] Tvrdík J. Differential Evolution with Competitive Setting of its Control Parameters. TASK Quarterly, 2007, 11, 169 - 179. [23] Tvrdík J., Habiballa H., Pavliska V. Matlab Program Library for Box-Costrained Global Optimization. APLIMAT 2007, Part I, 6th International Conference on Applied Math. Slovak University of Technology, Bratislava, 2007, 463 - 470.
Program Library available at http://albert.osu.cz/oukip/optimization/. [24] Tvrdík, J., Krivý, I. Competitive Self-adaptation in Evolutionary Algorithms, EUSFLAT 2007, September 11-14, Ostrava (to appear).