Fuzzy logic is known by many applications in various areas. A common denominator of them in most cases is the ability of FL to capture, in a certain sense, semantics of a part of natural language semantics. A crucial role is played by the, so called evaluative linguistic expressions and conditional statements containing them. The former are used in control, managerial decision-making, identification, etc. Typical examples of evaluative expressions are “very small, more or less medium, roughly big, extremely deep, more or less brief, about twenty five, approximately 1000, not small, not very big, roughly small or medium, quite roughly medium and/but not big”, etc. The expressions containing words “small, medium, big” can be taken as canonical.
Conditional statements consisting of evaluative expressions are in fuzzy logic called fuzzy IF-THEN rules, for example
IF obstacle is near AND car speed is big THEN break very much
Such a rule can be schematically written as
IF X je A1 AND … AND Xn je An THEN Y je B
where Xi is a variable representing objects (e.g., values of distance, depth, size, etc.) and Ai, Bi are the evaluative linguistic expressions. Sets of fuzzy IF-THEN rules are called rule bases or linguistic descriptions because they can play the role of a special text with specific meaning.
Linguistic descriptions (rule bases) are fundamental bearers of knowledge. They are used when describing behavior of systems, control or decision-making strategies, for identification, and in various other situations.
Linguistic descriptions are further used in very important approximate reasoning scheme:
Conditions: R1 := IF X1 is A11 AND … AND Xn is A1n THEN Y is B1,
……………………………………………………………................
Rm := IF X1 is Am1 AND … AND Xn is Amn THEN Y is Bm,
Observation: X1 is A’1 AND … AND Xn is A’n
______________________________________________________
Conclusion: Y is B’
The conditions comprise of the linguistic description. The A‘i‘s in the observation are, in general, certain modifications of the antecedents Ai of the rules (the part of the rule preceding the word THEN).
The knowledge is in natural language made more specific using generalized quantifiers that are expressions such as “most, many, a lot of, a few, few, a great deal of, large part of, small part of”, etc. Note that such quantifiers are in the literature on fuzzy sets called also fuzzy quantifiers. In linguistic theory, the above examples of generalized quantifiers fall into the class of intermediate quantifiers.
Intermediate quantifiers are used in special syllogisms (generalizations of Aristotle’s ones), for example:
All M are Y
2. Focus of our research
- elaboration of the formal theory of the meaning of evaluative linguistic expressions,
- elaboration of the formal theory of the meaning (linguistically specified) fuzzy IF-THEN rules and linguistic descriptions,
- formulation of the theory of generalized quantifiers in fuzzy logic,
- elaboration of the theory of intermediate quantifiers,
- development and study of various reasoning schemes in which natural language plays substantial role.
Note that the theory of linguistic descriptions can be divided into two directions: the first falls into the area of fuzzy approximation where linguistic descriptions are interpreted using the calculus of fuzzy relations. The second direction is based on the idea that sets of fuzzy IF-THEN rules form a special text.
3. Description of the main results
The theory of evaluative linguistic expressions
Using the fuzzy type theory we managed to model plausibly the semantics of evaluative expressions [12], [14], [16], [17], [26] [33]. The theory is based on detailed logical analysis of their meaning. Essential notion is linguistic context that is (in case of evaluating expressions) an interval of numbers [vL, vR] with a clearly distinguished central point vS, such that vL < vS R. The following figure demonstrates behavior of evaluative expressions in every context (in this case vL =0, vS =50, vR =100): small values are some values on the left side, part of it are very small values and still smaller part are extremely small values. The same is expressed using fuzzy sets in the middle of the figure.
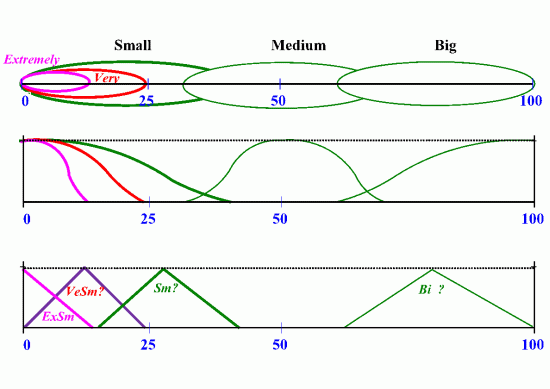
It can be also seen that triangle representation of evaluative expressions is wrong in any context (since, e.g., the value 5 is partially extremely small, partially also very small but not small at all which contradicts understanding to these expressions).
The theory of evaluative linguistic expressions is further applied to formalization of the meaning of fuzzy IF-THEN rules and linguistic descriptions [30], [35]. These rules are here taken conditional clauses of natural language consisting of evaluative expressions. We have developed special reasoning method (se below), and also a method for learning linguistic descriptions from the data [1], [4].
Another theory in which evaluative expressions play a crucial role is formal theory of intermediate quantifiers [12], [27]. These quantifiers are introduced naturally as special formulas expressing size of the universe by specific evaluative expressions. The paper [27] contains formal proofs of about 20 generalized Aristotle’s syllogisms that hold in this theory.
Perception-based logical deduction (PbLD)
This is essential method for finding conclusion on the basis of the above considered linguistic descriptions. It has been formalized first in predicate first-order fuzzy logic with evaluated syntax [3], [8], [10], [15]. Recently, it has been newly formalized in the frame of fuzzy type theory and in correspondence with the theory of evaluative expressions [5], [19], [24], [31], [32], [34]. The main idea is the following: a concrete measured value in specific context is perception that is identified with specific evaluative expression (in correspondence with the given linguistic description). The perception and linguistic description are used for derivation of a conclusion.
Our method offers results similar to the way how people derive conclusion on the basis of text linguistically describing some situation (hence the term linguistic description). There are numerous possible applications of PbLD in control, decision making, classification, and many others.
The basic behavior of PbLD is demonstrated below. The linguistic description is simple consisting of two fuzzy IF-THEN rules only:
1. IF X is small THEN Y is very big,
2. IF X is very big THEN Y is small.
PbLD can distinguish between both rules. Moreover, the less true is antecedent, the less is true is consequent, i.e., in case of Rule 1, the greater is X the smaller is Y, and vice-versa for Rule 2.
Click to see a flash demonstration of LFLC in SWF format.
The next demonstration shows behavior of PbLD when solving control/decision problem when avoiding obstacle. The situation is clear from the picture: a car should turn to the left, if the obstacle is very near and turn to the right, if the obstacle is near.
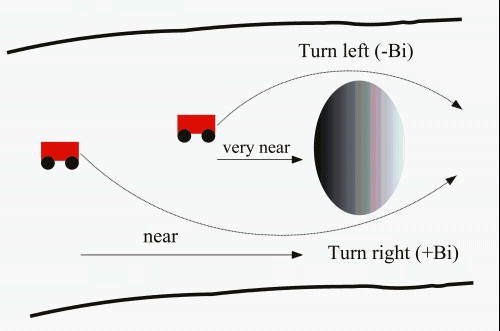
The PbLD method offers correct behavior such situations, as can be seen from the lower right part of the following demonstration. The x axis shows distance of the obstacle and y axis turn of the steering wheel (in degrees).
Click to see a flash demonstration of avoding the obstacle problem in SWF format.
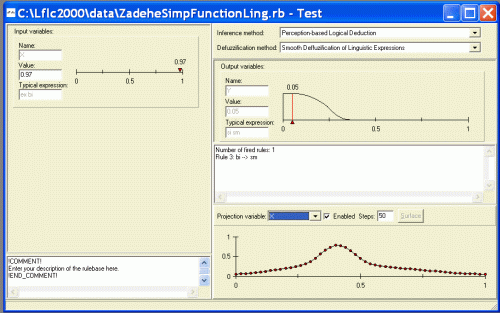
The classical PbLD may not always perform smoothly. This does not matter in decision making and also in most practical control problems. Sometimes, however, smooth behavior is required. Therefore, a special method called Smooth PbLD has been developed. This method keeps the essential properties of PbLD but at the same time is smooth and monotone. In the following figure, we demonstrate that it captures very well the meaning of linguistic description of the function that assigns “small values to small arguments, big values to medium arguments and small values to big arguments”. The result of smooth PbLD on the basis of such description can be seen in the lower right part of the following figure:
REFERENCES
[1] BĚLOHLÁVEK, R., NOVÁK, V. Learning rule base in linguistic expert systems. In Soft Computing. 2. vyd. 2002, sv.7, s.79-88, ISSN 1432-7643.[2] DVOŘÁK, A. On Linguistic Approximation in the Frame of LFLC. In IFSA'97 Prague. Proceedings. Prague : Academia, 1997. ISBN 80-200-0633-8. pp. 412-417.
[3] DVOŘÁK, A. Computational Properties of Fuzzy Logic Deduction. In Computational Intelligence. Theory and Applications. Berlin : Springer-Verlag, 1997. ISBN 3-540-62868-1. pp. 189-196.
[4] DVOŘÁK, A., NOVÁK, V. The Extraction of Linguistic Knowledge Using Fuzzy Logic and Generalized Quantifiers.. In Computational Intelligent Systems for Applied Research. Singapore : World Scientific, 2002. ISBN 9812380663. pp. 113-120.
[5] DVOŘÁK, A., NOVÁK, V. Fuzzy Type Theory as a Tool for Linguistic Analysis. In The Logica Yearbook 2006. Prague : Filosofia, 2007. ISBN 978-80-7007-254-7. pp. 51-61.
[6] DVOŘÁK, A., NOVÁK, V. On the Extraction of Linguistic Knowledge in Databases Using Fuzzy Logic. In Flexible Query Answering Systems. Recent Advances. Heidelberg : Physica-Verlag, 2001. ISBN 3-7908-1347-8. pp. 445-454.
[7] DVOŘÁK, A. On Linguistic Approximation in the Frame of Fuzzy Logic Deduction. In Soft Computing. 3. 1999, 2, pp.111-116, ISSN 1432-7643.
[8] DVOŘÁK, A. On Preselection of Rules in Fuzzy Logic Deduction. In International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems. 8. 2000, 5, pp.563-572, ISSN 0218-4885.
[9] DVOŘÁK, A., HABIBALLA, H., NOVÁK, V., PAVLISKA, V. The software package LFLC 2000 – its specificity, recent and perspective Applications. In Computers in Industry. 03. 2003, vol.51, pp.269-280, ISSN 0166-3615.
[10] DVOŘÁK, A., NOVÁK, V. Formal Theories and Linguistic Descriptions.. In Fuzzy Sets and Systems. 8. 2004, 1, pp.169-188
[11] DVOŘÁK, A., NOVÁK, V., PAVLISKA, V. Rules, Inferences and Robust Approximation at Work. In ERCIM News. 64. 2006, vol.2006, pp.31-32
[12] NOVÁK, V. Antonyms and Linguistic Quantifiers in Fuzzy Logic. In Fuzzy Sets and Systems. 2001, vol.124, pp.335-351, ISSN 0165-0114.
[13] NOVÁK, V.: Indeterminacy, Linguistic Semantics and Fuzzy Logic. Proc. Conf. Intelligent Systems: A Semiotic Perspective, Gathersburg, Maryland 1996, 95–100.
[14] NOVÁK, V.: Evaluating Linguistic Expressions and Their Role in the Design of the Fuzzy Control Strategy. 2nd Int. Symposium on Fuzzy Logic and Applications, Zurich 1997, ICSC Academic Press, Canada/Switzerland 1997, 89–94.
[15] NOVÁK, V.: Fuzzy IF-THEN rules in logical deduction and their learning form data. 4th Czech-Japan Seminar on Data Analysis and Decision Making under Uncertainty, Sept. 14-17, 2001, 96-107.
[16] NOVÁK, V. Transparent Model of Linguistic Trichotomy and Hedges. In Fourth European Congress on Intelligent Techniques and Soft Computing. 1996-09-02-1996-09-05 Aachen, SRN. Aachen: Verlag Mainz, 1996. pp. 35-39. ISBN 3--89653--187-5.
[17] NOVÁK, V. Fuzzy Logic Theory of Evaluating Expressions and Comparative Quantifiers. In IMPU'06. 2006-07-02-2006-07-05 Paris. Paris : Editions EDK, 2006. pp. 1572-1579. ISBN 2-84254-112-X.
[18] NOVÁK, V. Approximation Abilities of Perception-based Logical Deduction. In Third Conf. EUSFLAT 2003. 10. 9. 2003-12. 9. 2003 Zittau/Goerlitz, Germany. Zittau/Goerlitz : University of Applied Science at Zittau/Goerlitz, 2003. pp. 630-635. ISBN 3-9808089-4-7.
[19] NOVÁK, V. Perception-based Logical Deduction as Alternative Approximate Reasoning Method. In FUZZ-IEEE2005 The international Conference on FUZZY Systems. 2005-05-22-2005-05-25 Reno, Nevada, USA. Reno, Nevada, : IEEE (Computational Intelligence Society), 2005. pp. 1032-1037. ISBN ISBN 0-7803-9159-4.
[20] NOVÁK, V. Soft Computing Methods in Managerial Decision Making. In Proc. 7th Czech-Japan Seminar on Data Analysis and Decision Making Under Uncertainty. 2004-08-31-2004-09-02 Awai Yumebutai International Conference Center, Hyogo, Japan. Hyogo: Kansai Chapter of the Operations Research Society of Japan , 2004. pp. 63-68.
[21] NOVÁK, V. Is Crucial Role in Soft Computing Played by Words?. In Int. Panel Conference on Soft and Intelligent Computing. 1996-10-07-1996-10-07 Budapes, Maďarsko. Budapest : Technical University, 1996. pp. 223-228. ISBN 963-420-510-0.
[22] NOVÁK, V. Fuzzy logic deduction with words applied to ancient sea level estimation. In Fuzzy logic in geology. Amsterdam : Academic Press, 2003. ISBN 0-12-415146-9. pp. 301-336.
[23] NOVÁK, V. Fuzzy Relation Equations with Words. In Fuzzy Partial Differential Equations and Relational Equations. Heidelberg : Springer, 2004. ISBN 3-540-20322-2. pp. 167-185.
[24] NOVÁK, V. Perception-Based Logical Deduction. In Reusch, B. (ed.): Computational Intelligence, Theory and Applications. Berlin : Springer, 2005. ISBN 3-540-22807-1. s. 237-250.
[25] NOVÁK, V.: Mathematical fuzzy logic in modeling of natural language semantics. In P. Wang, D. Ruan, E. Kerre (Eds.) Fuzzy Logic - A Spectrum of Theoretical & Practical Issues. Berlin : Springer, 2007. pp. 145-182
[26] NOVÁK, V. A Comprehensive Theory of Trichotomous Evaluative Linguistic Expressions. Fuzzy Sets and Systems. 2008, vol 159, pp. 2939-2969.
[27] NOVÁK, V. A Formal Theory of Intermediate Quantifiers. Fuzzy Sets and Systems, 2008, vol. 159, pp. 1229-1246.
[28] NOVÁK, V. Modeling with words: Scholarpedia.
[29] NOVÁK, V., DVOŘÁK, A. A Model of Complex Human Reasoning in Fuzzy Logic in Broader Sense. In Fuzzy Sets and Systems. 2008,
[30] NOVÁK, V., KOVÁŘ, J. Linguistic IF-THEN Rules in Large Scale Application of Fuzzy Control. In Fuzzy If-Then Rules in Computational Intelligence: Theory and Applications. Boston : Kluwer, 2000. ISBN 0-7923-7820-2. pp. 223-241.
[31] NOVÁK, V., LEHMKE, S. Logical Structure of Fuzzy IF-THEN Rules. Fuzzy Sets and Systems. 2006, vol.157, pp.2003-2029, ISSN 0165-0114.
[32] NOVÁK, V., PERFILIEVA, I. On the Semantics of Perception-Based Fuzzy Logic Deduction. In Journal of Intelligent Systems. 2004, 19, pp.1007-1031, ISSN 0884-8173.
[33] NOVÁK, V., I. PERFILIEVA: Smooth Perception-Based Fuzzy Logic Deduction. Proc. Czech-Japan Seminar, Valtice 2003.
[34] NOVÁK, V. and I. PERFILIEVA: Evaluating Linguistic Expressions and Functional Fuzzy Theories in Fuzzy Logic. In: L. A. Zadeh and J. Kacprzyk (eds.): Computing with Words in Information/Intelligent Systems 1. Springer-Verlag, Heidelberg 1999, 383–406.
[35] NOVÁK, V., I. PERFILIEVA: Smooth Fuzzy Logic Deduction With Words. Proc. Int. Conf. Fuzzy Information Processing: Theories and Applications, Vol. II, Tsinghua University Press/Springer, Beijing 2003, 599-604.
[36] PERFILIEVA, I. Fuzzy IF-THEN Rules from Logical Point of View. In Reusch, B. (ed.): Computational Intelligence, Theory and Applications. 1. vyd. Heidelberg : Springer, 2005. ISBN 1615-3871. s. 691-697.


