This is special software integrated with LFLC 2000. It makes it possible to simulate fuzzy control of simple processes in a closed feedback loop: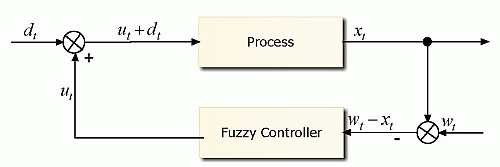
It is important to stress that the fuzzy controller in no way uses the differential equation. Its role in simulation is only to generate proper behavior of the process. The process remains for fuzzy controller a black box because the leading idea of fuzzy control is the following: we know, how the process should be controlled but the process itself is not known to us (or, its knowledge is not required). The scheme of fuzzy controller is in the following figure:
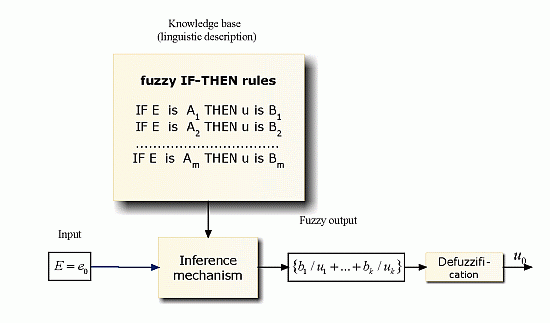
There are three main components of fuzzy controller: the knowledge base, inference mechanism, and defuzzification. There are several possibilities how these components can be realized. The “classical way” is to assign each fuzzy IF-THEN rule in the knowledge base a fuzzy relation (the rule is formed by triangular or trapezoidal fuzzy sets) and to represent the whole base by a global fuzzy relation obtained as interpretation of one of two possible forms: disjunctive (DNF) or conjunctive normal form (CNF). The inference mechanism is then a suitable projection of the fuzzy relation to obtain a fuzzy set that is finally defuzzified (usuall Center of Gravity; COG). The combination “DNF-COG” is in the literature called Mamdani fuzzy controller.
The leading idea of LFLCSim, however, is to implement linguistically oriented fuzzy logic control. This means that the knowledge base is formed by a linguistic description consisting of genuine linguistic IF-THEN rules. The inference mechanism is perception-based logical deduction and the defuzzification (that is here also necessary) is defuzzification of evaluative expressions (DEE) (for more detailed explanation, see [3], [4],[5]).
We distinguish the following types of fuzzy controller that are determined by the form of fuzzy IF-THEN rules in the linguistic description:
P- controller:
PD- controller:
PI- controller:
PID- controller:
where Et is error, dEt, d2Et are its first and second derivative, ut is control action, dut is its derivation and A, B, C, D are evaluative expressions.
Main functions of LFLCSim
- Simulation of control in a simple closed feedback loop using one of the above kinds of fuzzy logic controller.
- Manual testing of the process behavior.
The fuzzy controller in simulation can be of the following:
- linguistically oriented fuzzy logic controller, i.e., fuzzy IF-THEN rules are specified in pure linguistic form. The inference mechanism is perception-based logical deduction, defuzzification is one of DEE methods.
- standard fuzzy controller, i.e., fuzzy IF-THEN rules are specified using user defined fuzzy sets (usually triangle ones), the inference mechanism is fuzzy aproximation on the basis of DNF or CNF together with the defuzzification COG (or Mean of Maxima ; MOM).
Adaptation
LFLCSim enables also adaptation of fuzzy controller which leads to very precise control. This is achieved using a sophisticated routine which changes linguistic context depending on the actual distance from the set point.
Learning
The test of the process behavior can be utilized for manual simulation of successful control. The latter can be monitored and the obtained data used in learning of linguistic description (in connection with LFLC 2000). The learned description can subsequently be used in automatic fuzzy control.
REFERENCES
[1] DVOŘÁK, A., HABIBALLA, H., NOVÁK, V., PAVLISKA, V. The software package LFLC 2000 – its specificity, recent and perspective Applications. In Computers in Industry. 03. 2003, vol.51, pp.269-280, ISSN 0166-3615.
[2] NOVÁK, V. Foundations of fuzzy modeling (Základy fuzzy modelování). Praha: BEN-technická literatura, 2000. 166 pp. ISBN 80-7300-009-1 (in Czech).
[3] NOVÁK, V. Perception-Based Logical Deduction. In Reusch, B. (ed.): Computational Intelligence, Theory and Applications. Berlin : Springer, 2005. ISBN 3-540-22807-1. s. 237-250.
[4] NOVÁK, V.: Mathematical fuzzy logic in modeling of natural language semantics. In P. Wang, D. Ruan, E. Kerre (Eds.) Fuzzy Logic - A Spectrum of Theoretical & Practical Issues. Berlin : Springer, 2007. pp. 145-182
[5] NOVÁK, V., PERFILIEVA, I. On the Semantics of Perception-Based Fuzzy Logic Deduction. In Journal of Intelligent Systems. 2004, 19, pp.1007-1031, ISSN 0884-8173.


