Introduction
LFLC 2000 (Linguistic Fuzzy Logic Controller) is specialized software, which is based on deep results obtained in formal theory of fuzzy logic. It makes it possible to deduce conclusions on the basis of imprecise description of the given situation using fuzzy IF-THEN rules. The rules are interpreted either as fuzzy relations, or they can be taken as genuine linguistic expressions and interpreted using the original theory developed in IRAFM.
Sets of linguistically interpreted fuzzy IF-THEN rules are called linguistic descriptions. They can be understood as specific text describing the given process, decision, or classification situation. The users may thus work only with expressions of natural language without necessity to think how they are implemented. Hence, the computer behaves as if “partner” which understands the language of human user.
LFLC 2000 is written in C++ under Windows and it is fully object oriented system. The system is integrated with other software LFLCSim using which we can simulate simple control in closed feedback loop. LFLC2000 is also joined with MATLAB/Simulink so that simulation of wide class of systems is possible.
The purpose of LFLC
- Design of linguistic descriptions: LFLC makes possible to use various pre-defined evaluative linguistic expressions (e.g., small, about 5, more or less medium etc.) It has also means for an analysis of several properties of linguistic descriptions (sorting, detection of identical, inconsistent or redundant IF–THEN rules etc.). In addition to standard linguistic descriptions [4], it is also possible to use IF–THEN rules of Takagi–Sugeno type with consequents specified as singletons.
- Design and modification of user expressions: In addition to pre-defined linguistic expressions users can also define and use their own expressions in situations when standard ones are for some reasons insufficient.
- Testing of inference over designed linguistic descriptions: LFLC allows users to visualize the behavior of a linguistic description for various (crisp) observations. He/she can select various inference and defuzzification methods (see [4]) and look at projections with respect to individual variables or three-dimensional control surface. There is also information about IF–THEN rules fired and the most suitable linguistic expressions assigned to crisp values from input or output intervals.
- Learning of linguistic description from experimental data: LFLC implements two methods for learning of linguistic description from data sets. The first method is based on the ability to find proper evaluative linguistic expression corresponding to the given value. The resulting linguistic description should be used for finding conclusions using perception-based logical deduction [4].
The second possibility is based on theoretical results published in [6], [7] and it enables to find a linguistic description interpreted by disjunctive or conjunctive normal form [6] with the prescribed accuracy of approximation of the data understood as specification of some function.
Both fuzzy approximation techniques are constructed to deal with fuzzy numbers or fuzzy sets which partition the respective domain in such a way that their kernels do not overlap each other. Therefore, the learning can be designed similarly to the linguistic one after specifying the set of possible fuzzy sets for each variable. They are specified by so called user expressions, which are nonlinguistic fuzzy sets on respective domains. This gives a user an opportunity to make several decisions about accuracy and/or complexity on each axis.
Important data structures and algorithms
Next figure shows the hierarchy of the main classes of LFLC. There are classes for the representation of fuzzy sets (CFuzzySet and its derivatives), classes which allow assignments of fuzzy sets to linguistic expressions (CLinguisticSettings), classes for the representation of operations on truth degrees and induced operations on fuzzy sets (C1ArgOper, C2ArgOper and their derivatives), class which represents an overall linguistic description (CRuleBase) and several auxiliary classes.

instances of CLinguisticSettings are members of CRuleBase.
Representation of fuzzy sets
There are four basic types of fuzzy sets derived from CFuzzySet which can be distinguished by implementation of the membership function, namely discrete fuzzy sets, parametric fuzzy sets, fuzzy sets with membership function represented by means of α-cuts and general fuzzy sets with membership function defined using arbitrary function given by a user.
Operations on fuzzy sets are implemented by classes derived from C1ArgOper and C2ArgOper. Classes derived from C1ArgOper implement prefix operators, e.g. negation. Subclasses of C2ArgOper implement as their methods various types of intersections, unions, implications and differences of fuzzy sets. In this way e.g. intersection has no predefined t-norm, but it is possible to use any t-norm implemented by some subclass of C2ArgOper.
Representation of semantical rule
Representation of linguistic description
LFLC software system implements various inference and defuzzification methods. It allows a user to compare different combinations of them. Main inference methods are:
- Perception-based logical deduction [3], [4].
- Fuzzy approximation using disjunctive normal form (a linguistic description is used to characterize vaguely some crisp function; see [7]).
- Fuzzy approximation using conjunctive normal form (a linguistic description is also used to characterize a crisp function, but IF-THEN rules are interpreted as implications).
Main defuzzification methods implemented in LFLC are:
- Center of Gravity (COG),
- Mean of Maxima (MOM),
- Defuzzification of Evaluative Expressions (DEE),
- Simple Defuzzification of Evaluative Expressions,
- Smooth Defuzzification of Evaluative Expressions.
Recall that the DEE method is a special defuzzification method designed for use in conjunction with Perception-based Logical Deduction method.
User interface
The simplest way how to describe the user interface is to show some screenshots of the running application.
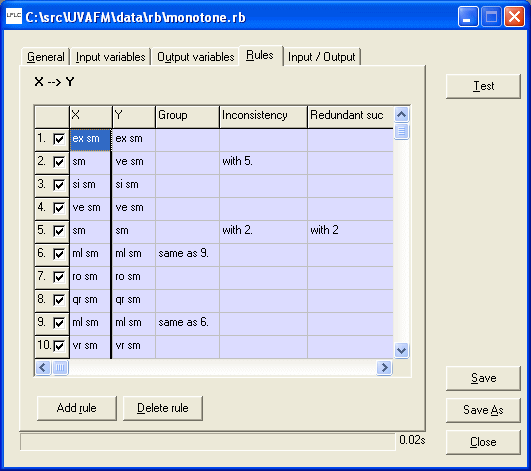
Next figure contains the “test screen” dialog where a user can test a behavior of the inference on the basis of the designed linguistic description. On the left hand side a user can interactively enter the crisp inputs to the inference for each input variable. On the bottom of left side he/she can see the input rulebase file; this is an ordinary text file.
On the right hand side of the dialog window, a user can change the defuzzification and inference methods (see [4]). Further he/she can see the output fuzzy set of the inference for previously entered crisp inputs together with the defuzzified value and also the number of fired rules in the inference. Last but not least item is the projection over one chosen variable.
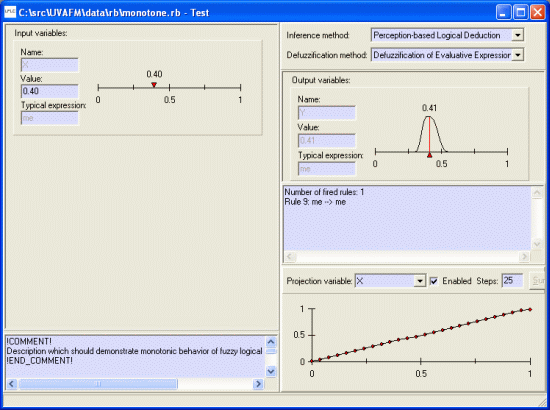
The user can also define uniform distribution of triangular membership functions (this is useful for various kinds of applications).
The last figure of user interface shows a screen for learning of linguistic description from numerical data. A user first imports file with numerical data, then choose some learning method. Linguistic description is consequently generated.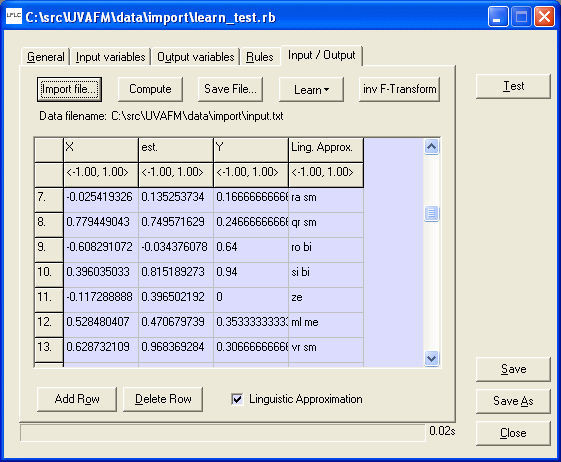
Interface to other software systems
The COM Object RBaseCOM is installed and registered into MS Windows system, hence any other application can make use of services provided by it.
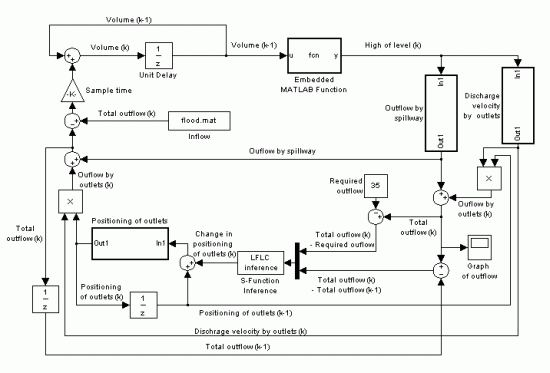
A MATLAB S-Function for Simulink package has also been developed, which provides link between LFLC and MATLAB/Simulink software products. It uses the COM Object mentioned above, which runs in the background and a user of MATLAB environment need not worry about it. This S-Function is very useful, because it enables simulation, e.g. of control of various kinds of processes using the LFLC system in MATLAB/Simulink software system. On Figure below you can see simulation scheme of the outflow of Těrlicko bay (one of applications/simulations designed in our institute) which uses mentioned S-Function as main control component.
Demonstration
Basic Usage of LFLC.swf
References:
[[1] NOVÁK, V., PERFILIEVA, I., MOČKOŘ, J.: Mathematical Principles of Fuzzy Logic. Kluwer, Boston, 1999.
[2] NOVÁK, V.: A Comprehensive Theory of Trichotomous Evaluative Linguistic Expressions. In S. Gottwald, P. Hájek, U. Höhle, and E. P. Klement, editors, Proc. of 26th Linz Seminar on Fuzzy Set Theory. (to appear). Research Report No. 71.
[3] NOVÁK, V.: Mathematical fuzzy logic in modeling of natural language semantics. In P. Wang, D. Ruan, E. Kerre (Eds.) Fuzzy Logic - A Spectrum of Theoretical & Practical Issues. Berlin : Springer, 2007. pp. 145-182
[4] NOVÁK, V., PERFILIEVA, I.: On the semantics of perception–based fuzzy logic deduction. International Journal of Intelligent Systems, 19:1007–1031, 2004.
[5] NOVÁK, V., LEHMKE, S.: Logical structure of fuzzy IF–THEN rules. Fuzzy Sets and Systems, 157:2003–2029, 2006.
[6] PERFILIEVA, I.: Normal forms for fuzzy logic functions and their approximation ability. Fuzzy Sets and Systems, 124:371–384, 2001.
[7] PERFILIEVA, I.: Fuzzy relations, functions, and their representation by formulas. Neural Network World, 10:877–890, 2000.


