Automated proving in fuzzy logic

1 Introduction

The first-order Fuzzy Predicate Logic with evaluated syntax (Ev_L) forms a powerful generalization of classical two-valued logic [7]. This generalization brings several hard problems with automated theorem proving especially when utilizing the widely used resolution principle. The resolution-based reasoning in its usually preferred way of application uses the clausal form formulas. We will present the refutational resolution theorem proving system for FPL (RRTP_FPL) based on general (non-clausal) resolution principle in first-order logic (FOL) [1]. The below presented implementation of non-clausal resolution theorem prover for Ev_L has the title Fuzzy Predicate Logic GEneralised Resolution Deductive System (FPLGERDS) [4]. In order to use an efficient form of the resolution principle [2] we have to extend the standard notion of a proof (provability degree) with the notion of refutational proof (refutation degree).

General resolution for Ev_L (GR_FPL)

where σ = MGU(A) is the most general unifier of atoms A = { G₁, ... , G_k ,G´₁, ... ,G´_n } , G = G₁σ.

Details of the theory could be found in the referenced works. (extended unification [5], refutational proof and degree [4], resolution strategies for efficient inference [6]).

2 Purpose of the FPLGERDS

Above mentioned theoretical framework is already implemented in a computer application called Fuzzy Predicate Logic Generalized Resolution Deductive System (FPLGERDS). It enables to edit knowledge bases of Fuzzy Predicate Logic with evaluated syntax and performing deduction on required goals. Figure 1 shows FPLGERDS's GUI. It is essentially divided into the input panel (knowledge base formed by fuzzy predicate logic formulas with evaluation degree and the query formed by one fuzzy predicate logic formula) and the output panel (results of inference with various details like axioms, resolvents, unsimplified resolvents, number of resolvents etc.). Axioms are written in common mathematical notion and results of inference provide proof sequence with marked premises, which particular resolvent was derived from. It can present the terms used for unification in goal's variables (PROLOG like). It also offers several types of resolution strategies as visible on the upper panel and unification and resolution restrictions as well as statistics of inference.

User environment enables to work with two essential panels: Editor and Output. Editor is intended for editing knowledge bases and goals while Output shows results of inference. Special axioms and goals have the format described in fig. 2. Every special axiom or goal is followed by semicolon. Special axioms consist of the formula and optional syntactic degree. Syntactic degree ranges from 0 to 1. If no syntactic degree is given then implicit degree of 1 is assigned. A goal cannot have syntactic degree. If all axioms have no degree or their degree is equal to 1, then the inference process degrades to classical two-valued logic. Output serves for observation of inference results. User can choose from various types of output information. The essential information consists of the axiom and resolvent list together with identification of every formula and identification of source formulas for resolvents. If a refutation is found the word "YES" is printed with appropriate refutation degree.

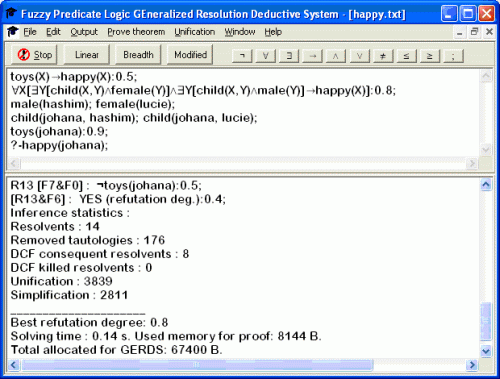
Figure 1: Frame of GERDS

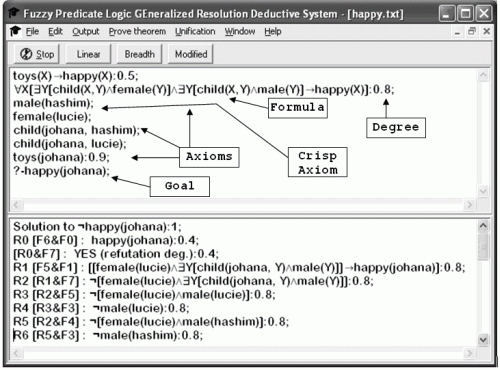
Figure 2: Structure of Editor Panel

Figure 3: Structure of Output Panel

3 Demonstration

FPLGERDS allows to edit knowledge bases and perform inference upon them. It enables to set up custom preferences which depend mainly on crisp/fuzzy type of formulas. If crisp knowledge base is supported then it is possible to use standard inference strategies like Set of Support strategy while on fuzzy knowledge bases these setting have not sense. These strategies are not complete under fuzzy logic. User menu includes standard items:

• File menu - creating, loading and saving of knowledge bases
• Edit menu - copying, cutting, inserting the text in Editor and Output panel
• Window menu - arranging of the windows (the application allows to work with several knowledge bases simultaneously)

User can use menus for controlling the inference. Output menu (format specifications):

• Axioms - the list of axioms and goals (inputs of inference) at the beginning of output
• Progress - checking on adds every produced resolvent into output
• Sources - includes identification marks for premises of resolution
• Resolvents - produces summarization of all resolvents produced during the inference
• Time, Memory - incorporates time and space requirements for inference
• Unsimplified - every resolvent is additionally printed in raw form without any simplification (no application of rewrite rules for F, T)
• Statistics - prints at the end of output number of produced resolvents, removed tautologies, DCF consequent resolvents, unifications and simplifications.
• DCF - adds every successful application of DCF algorithm (with identification of resolvent which caused DCF)
• Interactive - when checked off the output information is printed only when inference finishes and results are stored also to the file named with current knowledge base name and extension + .out; when checked on all results are printed immediately (be aware of outputs longer than 64 kBytes - they will be truncated and it should be used non-interactive setting); when measuring time complexity of the inference use non-interactive setting since printing significantly affects the time (for detailed outputs)

Prove theorem (controlling the inference)

• Stop - stops the inference before completion
• DCF limit - sets number of steps before the DCF algorithm will be stopped
• Linear search - starts the inference by linear strategy (not complete!)
• Breath-first search - starts the inference searching completely for every proof (complete upon unification with every possible atom)
• Modified linear search - linear strategy starting from not only goal, but every axiom and goal (not complete, but better than linear search)
• Trivial check only - filtrates resolvents by checking exact symbolic representation
• DCF - performs DCF algorithm (checks if resolvent is a consequence)
• DCF + Kill - performs DCF and also DCF Kill technique (any added resolvent may "kill" other resolvents - logical consequences)
• Without restr. strategy - no crisp inference strategy is applied (fuzzy knowledge bases)
• Filtration strategy - Filtration strategy is applied (use only for crisp knowledge bases)
• Support set strategy - Support Set strategy is applied (use only for crisp bases)

Unification (controlling the unification)

• Quantification on - off cause treating of variables to be universally quantified (ignoring quantifier); use for more efficient inference if no existentiality is required
• General cut - every unifiable atom in premises is removed
• Exit on first unused - finishes generation of resolvents on two premises on first atomic formula (use only for crisp bases - for fuzzy logic such inference is not complete!)
• Exit on first match - finishes generation of resolvents from two premises on first unifiable atomi (use for crisp bases - for fuzzy logic inference is not complete!)
• Exit on last match - generation of all possible resolvents on all atoms in two premises
• One refutation - searches only for first refutation (use only for crisp knowledge bases - for for fuzzy logic such inference is not complete!)
• All refutations - searches for all possible refutations upon selected strategy

4 Important algorithms and data structures

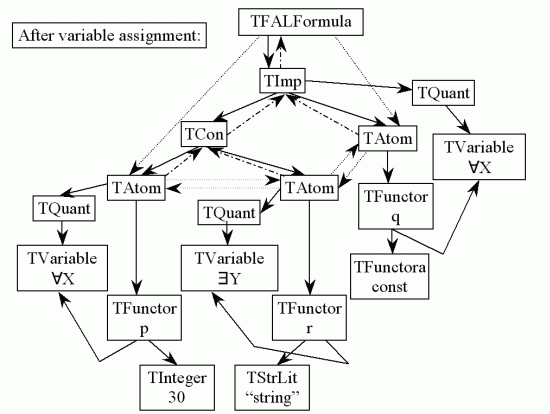
In contrast with clausal resolution prover the implementation of non-clausal prover requires more complex pointer-based data structures for internal formula representation. It could be observed from Figure 4, how the formula data structure is constructed. After compilation the syntactical tree is constructed without variable occurrences links to specific quantifier. The hierarchy of syntactical elements could be specified in Backus-Naur form. Abstract class TSub represents general subformula of FOL, which has its specifications according to type of logical connective (e.g. TCon - conjunction). Once the original tree is built the postprocessing phase may continue. Its main aim is to establish links (pointers) to appropriate quantifiers, to evaluate polarities of subformulas and to evaluate infix operators in the formula. Inference engine is based on general resolution rule procedure for production of resolvent on two formulas of FOL. The base procedure controlling the process tries to resolve upon all possible premises (it contains also filtrating mechanism of resolution strategies). It checks the consistency of the axiom set with negated query formula.

Figure 4: Example of formula data structure

The core procedure performs the general resolution rule. Formation of resolvent is relatively simple and requires only formation of premise copies and unification procedure. If the unification exists then it is possible to link copies of premises by disjunction (TDis object) and to substitute terms generated by unification (there is no need to replace all occurrences but only quantifier object in one memory cell). DCF may use existing resolution procedure since self-resolution is special case.

References

[1] BACHMAIR, L., GANZINGER, H. A theory of resolution. Tech. rep.: Max-Planck-Institut, 1997

[2] HABIBALLA, H., NOVAK, V. Fuzzy General Resolution. In Aplimat 2002. Bratislava : SJF STU, 2002. pp. 199-206. ISBN 80-227-1654-5. Download Research report 47.

[3] HABIBALLA, H.: Resolution Based Reasoning in Description Logic. In ZNALOSTI 2006. 1.-3.2.2006. Hradec Kralove : FIM UHK, 2006. pp. 106-117. ISBN 80-248-1001-8. Download Research report 64.

[4] HABIBALLA, H. Non-clausal Resolution in Fuzzy Predicate Logic with Evaluated Syntax (background and implementation). In The Logic of Soft Computing IV. 5.10.2005-7.10.2005 Ostrava. Ostrava : Ostravska Univerzita, 2005. pp. 51-54. Download Research report 70.

[5] HABIBALLA, H. Non-clausal Resolution Theorem Proving for Fuzzy Description Logic. In SOFSEM 2006. 2006-01-21-2006-01-27 Merin. Praha : Institute of Computer Science, Czech Academy of Sciences, 2006. pp. 1-12. ISBN 80-903298-4-5

[6] HABIBALLA, H.: Resolution strategies for fuzzy predicate logic with evaluated syntax. In ZNALOSTI 2007. 2006-02-21-2006-02-23 Ostrava. Ostrava : VSB-TUO, 2007. pp. 201-212. ISBN 978-80-248-1279-3.

[7] NOVAK, V., PERFILIEVA, I., MOCKOR, J. Mathematical Principles of Fuzzy Logic. Boston/Dordrecht/London : Kluwer Academic publishers, 1999. 320 pp. ISBN 0-7923-8595-0.